আজকে আমাদের আলোচনার বিষয় e = Emax sin (t) সমীকরণ প্রতিপাদন
e = Emax sin (t) সমীকরণ প্রতিপাদন

e = Emax sin (t) সমীকরণ প্রতিপাদন
৫.৪ নং চিত্রে প্রদর্শিত সর্বত্র সমান চৌম্বক ক্ষেত্রে অবস্থিত ‘n’ সংখ্যক প্যাচবিশিষ্ট একটি আয়তাকার কয়েল বিবেচনা করা যাক যা কি না ” রেডিয়ান/সেকেন্ড কৌণিক বেগে বামাবর্তে ঘুরছে। এ কয়েলে আবিষ্ট ই.এম.এফ. সাইনোসয়ডাল বা তরঙ্গাকৃতি হবে।
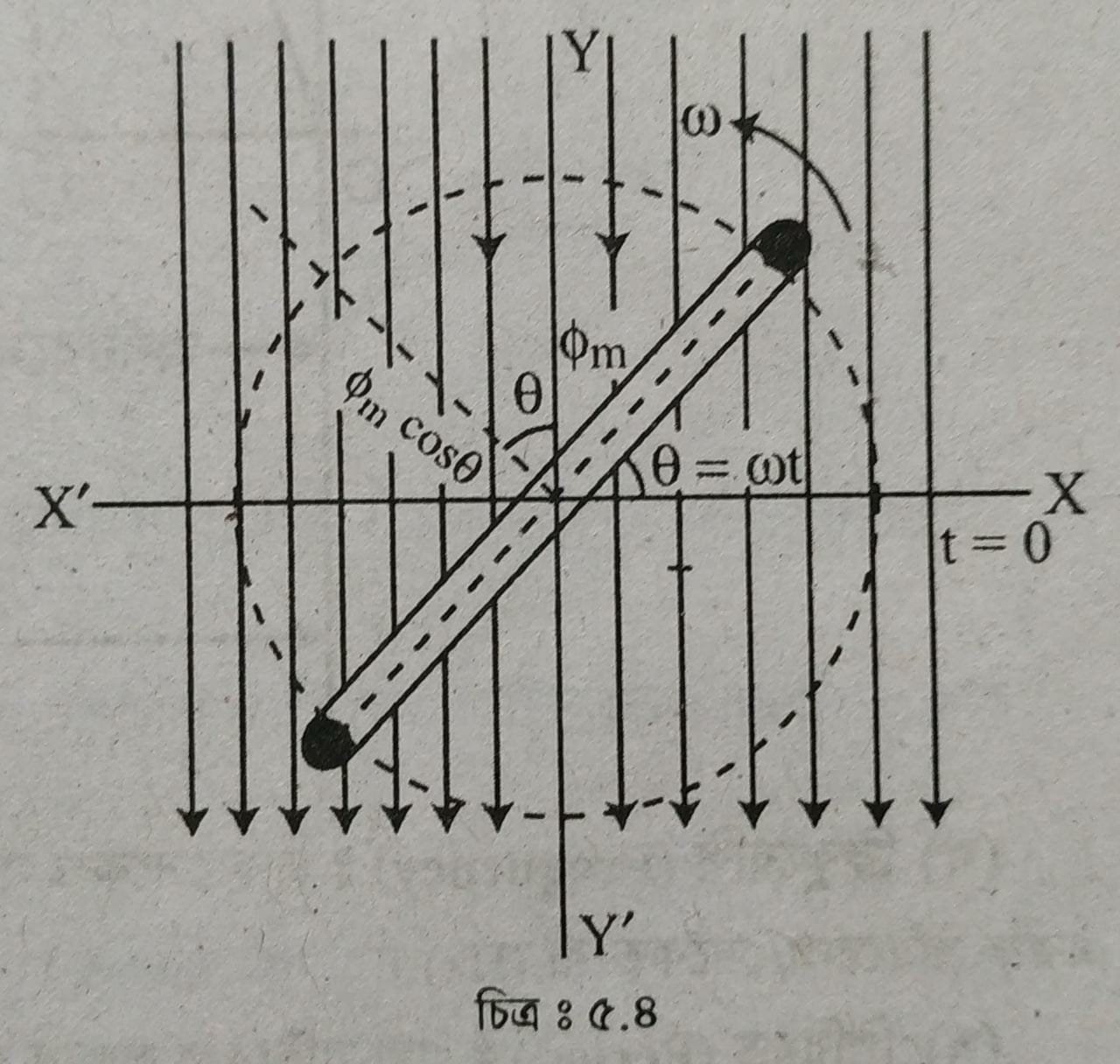
মনে করি, একটি কয়েল পরিবাহী চুম্বক ক্ষেত্রে XX´ অক্ষ বরাবর অবস্থান করছে এবং চুম্বক ক্ষেত্রের ফ্লাক্সের দিক YY অক্ষ বরাবর। কয়েলের XX’ অবস্থানে কয়েলের সাথে সংশ্লিষ্ট ফ্লাক্স-এর সর্বোচ্চ মান pmax এবং কয়েল পরিবাহী YY’ অবস্থানে থাকলে সংশ্লিষ্ট ফ্লাক্স সর্বনিম্ন হবে।
এখন ধরা যাক, । সেকেন্ড সময়ে কয়েলটি বামাবর্ত (Anti-clockwise direction) ঘুরে 8° = ot অবস্থানে পৌঁছায়। এ অবস্থানে পরিবাহীর উপর ক্রিয়াশীল ফ্লাক্সের দুটি উপাংশ থাকে, যথা :
১। Omax sin Cot উপাদানটি কয়েলের তলের সমান্তরাল। এ উপাদানটি কয়েলে কোন ই.এম.এফ আবিষ্ট করে না ।
২। Omarcos cot উপাদানটি কয়েলের তলের উপর লম্ব। এ উপাদানটি কয়েলে ই.এম.এফ আবিষ্ট করে ।
সুতরাং যেকোন সময়ে সমগ্র কয়েলের ফ্লাক্স লিংকেজ
= No x + cosot
ফ্যারাডের সূত্রানুযায়ী, একটি কয়েলের ই.এম.এফ আবিষ্টতা, কয়েলের ফ্লাক্স লিংকেজের পরিবর্তনের হারের সমান। অতএব, বিবেচনাধীন মুহূর্তে ই.এম এফ (e) হবে
‘e’-এর মান সর্বোচ্চ (Em) হবে, যখন sinût = 1 হবে, অর্থাৎ যখন XX’-অ্যাক্সিস হতে বামাবর্তে কয়েলটি 90° ঘুরে যাবে । : Emax = ON O (ii)
সুতরাং (i) নং সমীকরণ থেকে পাই,
.. e = Emax sinot
[:: Emax = ON O max ] (iii)
অথবা,
e = Emax sine. এটি পরিষ্কার যে, কয়েলে আবিষ্ট ই.এম.এফ সাইনোসোয়ডাল অর্থাৎ ই.এম.এফ এর তাৎক্ষণিক মান (Instantaneous value)
সময় কোণের (ot অথবা 6) সাইন ফাংশন অনুযায়ী পরিবর্তিত হয়। যদি কোন লোডের আড়াআড়িতে এ অল্টারনেটিং ভোল্টেজ (e = Emax sinot) প্রয়োগ করা হয়, তবে সার্কিটে অল্টারনেটিং কারেন্ট প্রবাহিত হবে, যা সাইনুসোয়ডালভাবে অর্থাৎ সাইন ল’ অনুযায়ী পরিবর্তিত হবে ।
কারেন্টবাহী সমান্তরাল পরিবাহীর মধ্যে বল নিয়ে বিস্তারিত :
