ম্যাক্সওয়েলের উপপাদ্য দিয়ে সমস্যার সমাধান ক্লাসটি ডিজিটাল “ইলেকট্রিকাল সার্কিট- ১ [ Electrical Circuit-1 ]” কোর্সের “Chapter 3 (Circuit Theorem )” অধ্যায়ে পড়ানো হয় | এই ক্লাসটি বাংলাদেশ কারিগরি শিক্ষা বোর্ড [Bangladesh Technical Education Board] এর পলিটেকনিক [Polytechnic] ডিসিপ্লিন এর ডিপ্লোমা ইন ইলেক্ট্রিক্যাল [Diploma in Electrical], “২য় সেমিস্টার, ইলেকট্রিকাল [ 2nd Semester, Electrical ]” এ পড়ানো হয়।
ম্যাক্সওয়েলের উপপাদ্য দিয়ে সমস্যার সমাধান
ম্যাক্সওয়েলের তত্ত্বের ভিত্তি হল উপরোক্ত চারটি সমীকরণ:
1. বৈদ্যুতিক ক্ষেত্র হিসাবে সম্ভাব্য হতে পারে ( ই প্রশ্নঃ) এবং ঘূর্ণি ( ই বি), সুতরাং, মোট ক্ষেত্র শক্তি ই=ই প্রশ্নঃ +ই বি। যেহেতু ভেক্টরের প্রচলন ই প্রশ্নঃ শূন্যের সমান (দেখুন (137.3)) এবং ভেক্টরের প্রচলন ই বি এক্সপ্রেশন (137.2) দ্বারা নির্ধারিত হয়, তারপরে মোট ক্ষেত্রের তীব্রতা ভেক্টরের প্রচলন
এই সমীকরণটি সূত্রগুলি দেখায় বৈদ্যুতিক ক্ষেত্র না শুধুমাত্র হতে পারে বৈদ্যুতিক চার্জ, তবে সময়ের পরিবর্তিত চৌম্বকীয় ক্ষেত্রগুলিও।
2. সাধারণ ভেক্টর সঞ্চালন উপপাদ্য এইচ (দেখুন (138.4)):
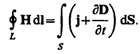
এই সমীকরণটি দেখায় যে চৌম্বকীয় ক্ষেত্রগুলি চলমান চার্জ (বৈদ্যুতিক স্রোত) দ্বারা বা বৈদ্যুতিক ক্ষেত্রগুলি পরিবর্তনের মাধ্যমে উত্তেজিত হতে পারে।
৩. মাঠের জন্য গাউস উপপাদ্য ডি (দেখুন (89.3)):
যদি চার্জটি বদ্ধ ঘনত্বের সাথে অবিচ্ছিন্নভাবে একটি বদ্ধ পৃষ্ঠের ভিতরে বিতরণ করা হয় r, তারপরে সূত্রটি (139.1) হিসাবে লেখা যেতে পারে
![]()
৪. মাঠের জন্য গাউস উপপাদ্য দ্য (দেখুন (120.3)):
সুতরাং, অবিচ্ছেদ্য আকারে ম্যাক্সওয়েল সমীকরণের সম্পূর্ণ সিস্টেম:
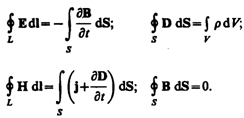
ম্যাক্সওয়েলের সমীকরণগুলিতে অন্তর্ভুক্ত মানগুলি স্বতন্ত্র নয় এবং তাদের মধ্যে নিম্নলিখিত সম্পর্ক বিদ্যমান (আইসোট্রপিক নন-ফেরোলেলেকট্রিক এবং নন-ফেরোম্যাগনেটিক মিডিয়া):
যেখানে ই 0 এবং মি 0 – যথাক্রমে বৈদ্যুতিক এবং চৌম্বকীয় ধ্রুবক, ই এবং মি – যথাক্রমে ডাইলেট্রিক এবং চৌম্বকীয় ব্যাপ্তিযোগ্যতা, ছ – পদার্থের সুনির্দিষ্ট পরিবাহিতা।
ম্যাক্সওয়েলের সমীকরণ থেকে এটি এসেছে যে বৈদ্যুতিক ক্ষেত্রের উত্সগুলি হয় বৈদ্যুতিক চার্জ হতে পারে, বা চৌম্বকীয় ক্ষেত্রগুলি সময়ের সাথে পরিবর্তিত হতে পারে এবং চৌম্বকীয় ক্ষেত্রগুলি হয় বৈদ্যুতিক চার্জ (বৈদ্যুতিক স্রোত) সরানো বা বৈদ্যুতিক ক্ষেত্রগুলি পরিবর্তনের মাধ্যমে উত্তেজিত হতে পারে। ম্যাক্সওয়েলের সমীকরণ বৈদ্যুতিক এবং চৌম্বকীয় ক্ষেত্রে সম্মিলিত নয়। প্রকৃতির প্রকৃতপক্ষে বৈদ্যুতিক চার্জ থাকলেও কোনও চৌম্বকীয় চার্জ হয় না এই কারণে এটি ঘটে।

স্থির ক্ষেত্রগুলির জন্য (E \u003dকনস্টেট এবং খ \u003dconst ) ম্যাক্সওয়েল সমীকরণ ফর্ম গ্রহণ করবে
অর্থাত এক্ষেত্রে কেবল বৈদ্যুতিক চার্জগুলি বৈদ্যুতিক ক্ষেত্রের উত্স, কেবল চালন স্রোতগুলি চৌম্বকীয় ক্ষেত্রের উত্স। এই ক্ষেত্রে, বৈদ্যুতিক এবং চৌম্বকীয় ক্ষেত্রগুলি একে অপরের থেকে স্বতন্ত্র, যা আমাদের আলাদাভাবে অধ্যয়ন করতে দেয় স্থায়ী বৈদ্যুতিক এবং চৌম্বকীয় ক্ষেত্র।
ভেক্টর বিশ্লেষণ থেকে পরিচিত স্টোকস এবং গাউসের উপপাদ্য ব্যবহার করা
কল্পনা করতে পারেন ডিফারেন্সিয়াল আকারে ম্যাক্সওয়েলের সমীকরণের সম্পূর্ণ সিস্টেম (মহাকাশের প্রতিটি বিন্দুতে ক্ষেত্রের বৈশিষ্ট্য নির্ধারণ):
যদি চার্জ এবং স্রোতগুলি অবিচ্ছিন্নভাবে স্থানগুলিতে বিতরণ করা হয় তবে ম্যাক্সওয়েল সমীকরণের দুটি রূপই – অবিচ্ছেদ্য এবং ডিফারেনশিয়াল – সমান। যাইহোক, যদি সেখানে বিচ্ছিন্নতা উপরিভাগ থাকে – এমন পৃষ্ঠতল যার উপর ভিত্তি করে মাঝারি বা ক্ষেত্রগুলির বৈশিষ্ট্যগুলি ধাপে পরিবর্তিত হয়, তবে সমীকরণগুলির অবিচ্ছেদ্য রূপটি আরও সাধারণ।
ডিফারেন্সিয়াল ফর্মের ম্যাক্সওয়েলের সমীকরণগুলি ধরে নেয় যে স্থান এবং সময়ের সমস্ত পরিমাণ ক্রমাগত পরিবর্তিত হয়। ম্যাক্সওয়েলের সমীকরণের উভয় রূপের গাণিতিক সমতুল্যতা অর্জন করতে, ডিফারেনশিয়াল ফর্মটি পরিপূরক হয় সীমানা শর্ত যা দুটি মিডিয়ার মধ্যবর্তী ইন্টারফেসে বৈদ্যুতিন চৌম্বক ক্ষেত্র দ্বারা সন্তুষ্ট হতে হবে। ম্যাক্সওয়েলের সমীকরণের অবিচ্ছেদ্য রূপে এই শর্ত রয়েছে। তারা এর আগে পর্যালোচনা করা হয়েছে:
(প্রথম এবং শেষের সমীকরণগুলি ইন্টারফেসে কোনও নিখরচায় চার্জ বা চালনের স্রোত না পাওয়া ক্ষেত্রে সম্পর্কিত)।
বৈদ্যুতিন এবং চৌম্বকীয় ক্ষেত্রগুলির জন্য সর্বাধিক সাধারণ সমীকরণ হ’ল ম্যাক্সওয়েলের সমীকরণ বিশ্রাম পরিবেশ। তারা যান্ত্রিকবিদ্যায় নিউটনের আইন হিসাবে তড়িৎচুম্বকত্বের তত্ত্বে একই ভূমিকা পালন করে। এটি ম্যাক্সওয়েলের সমীকরণ থেকে অনুসরণ করে যে একটি বিকল্প চৌম্বকীয় ক্ষেত্র সর্বদা এর দ্বারা উত্পাদিত বৈদ্যুতিক ক্ষেত্রের সাথে সম্পর্কিত এবং একটি বিকল্প বৈদ্যুতিক ক্ষেত্র সর্বদা এর দ্বারা উত্পাদিত চৌম্বকীয় ক্ষেত্রের সাথে যুক্ত থাকে, অর্থাত্ বৈদ্যুতিক এবং চৌম্বকীয় ক্ষেত্রগুলি একে অপরের সাথে যুক্ত থাকে – তারা একটি একক গঠন করে বৈদ্যুতিন চৌম্বক ক্ষেত্র.
বায়াস কারেন্ট অথবা শোষণ বর্তমান – বৈদ্যুতিক আনয়ন পরিবর্তনের হারের সাথে সরাসরি আনুপাতিক একটি মান। এই ধারণাটি ধ্রুপদী বৈদ্যুতিনবিদ্যায় ব্যবহৃত হয়।
বৈদ্যুতিন তত্ত্বের নির্মাণে জে কে ম্যাক্সওয়েল পরিচয় করিয়ে দিয়েছিলেন চৌম্বকীয় ক্ষেত্র.
পক্ষপাতের প্রবর্তনের ফলে চৌম্বকীয় ক্ষেত্রের সঞ্চালনের অ্যাম্পিয়ার সূত্রে বৈপরীত্য দূর করার অনুমতি দেওয়া হয়েছিল, যা সেখানে পক্ষপাতের বর্তমান যুক্ত করার পরে, সামঞ্জস্যপূর্ণ হয়ে ওঠে এবং শেষ সমীকরণটি তৈরি হয়েছিল, যা সঠিকভাবে (শাস্ত্রীয়) তড়িৎবিদ্যার সমীকরণের সিস্টেমটি বন্ধ করতে দেয়।
কড়া কথায় বলতে গেলে, পক্ষপাতের বর্তমান নয় বৈদ্যুতিক শকতবে বৈদ্যুতিক স্রোতের মতো একই ইউনিটে পরিমাপ করা হয়।

ম্যাক্সওয়েলের উপপাদ্য দিয়ে সমস্যার সমাধান নিয়ে বিস্তারিত :
আরও দেখুনঃ
