আজকে আমাদের আলোচনার বিষয় সার্কিট বিশ্রেষস্ অনুশীলনী ৩
সার্কিট বিশ্রেষস্ অনুশীলনী ৩
অতি সংক্ষিপ্ত প্রশ্নোত্তর :
১। কারশফের সূত্র কয়টি ও কী কী ?
উত্তর :- কারশফের সূত্র দুটি, যথা- (ক) কারেন্টের সূত্র (খ) ভোল্টেজের সূত্র।
২। ম্যাক্সওয়েল লুপ কারেন্ট থিওরেম কোন ধরনের সার্কিটে উপযোগী ?
উত্তর :- পাশাপাশি কতকগুলো সংযুক্ত লুপ সার্কিট বিশিষ্ট নেটওয়ার্কে বিভিন্ন শাখা কারেন্টের মান ও দিক বের করতে কারশফ সূত্রের পরিবর্তে লুপ বা মেশ কারেন্ট পদ্ধতি অর্থাৎ ম্যাক্সওয়েল থিওরেম পদ্ধতি উপযোগী ।
৩। ম্যাক্সওয়েল থিওরেমের সুবিধা লেখ।
উত্তর :- এ পদ্ধতির বড় সুবিধা হচ্ছে এই যে, একটা নেটওয়ার্কের সমাধানের জন্যে সমীকরণের সংখ্যা কম রাখা যায়।
৪। কারশফের প্রথম সূত্র বা কারেন্ট সূত্র কী ?
উত্তর :- কোনো বৈদ্যুতিক নেটওয়ার্কে এক বিন্দুতে মিলিত কারেন্টসমূহের বীজগাণিতিক যোগফল শূন্য হয়।
৫। কারশফের দ্বিতীয় সূত্র বা ভোল্টেজের সূত্র কী ?
উত্তর :- কোনো ঘেরা বা বদ্ধ (Closed) বৈদ্যুতিক সার্কিটে সকল ই.এম.এফ (E.M.F) এবং সকল ভোল্টেজ ড্রপের
বীজগাণিতিক যোগফল শূন্য হয়।
৬। থেভেনিন’স নেটওয়ার্কে ই.এম.এফ-এর উৎসগুলো কীসের দ্বারা স্থলাভিষিক্ত হয় ?
উত্তর :- ই.এম.এফ এর উৎসগুলো এদের সমতুল্য অভ্যন্তরীণ রেজিস্ট্যান্স দ্বারা স্থলাভিষিক্ত হয়।
৭। লিনিয়ার (Linear circuit) সার্কিট কী ?
উত্তর :- লিনিয়ার সার্কিট এমন একটি সার্কিট, যার প্যারামিটারগুলো ধ্রুব থাকে অর্থাৎ ভোল্টেজ এবং কারেন্টের পরিবর্তনেও প্যারামিটারগুলোর পরিবর্তন হয় না ।
৮। ‘থেভেনিন’স থিওরেম’-এ “ওপেন সার্কিট ভোল্টেজ” বলতে কী বুঝায় ?
উত্তর :- যে সার্কিটে ‘থেভেনিন’স থিওরেম’ প্রয়োগ করতে হবে, সেই সার্কিটের লোড বিচ্ছিন্ন করার পরে সার্কিটের খোলা প্রান্তদ্বয়ের মধ্যবর্তী ভোল্টেজকে ‘ওপেনসার্কিট ভোল্টেজ’ বলা হয়।
৯। একাধিক ই.এম.এফ উৎসবিশিষ্ট সার্কিট কোন সূত্র দ্বারা সমাধান করা হয় ?
উত্তর :- সুপারপজিশন সূত্র দ্বারা।
১০। ম্যাক্সিমাম পাওয়ার ট্রান্সফার থিওরেম অনুযায়ী লোডে কখন সর্বোচ্চ পাওয়ার ট্রান্সফার হয় ?
উত্তর :- ম্যাক্সিমাম পাওয়ার ট্রান্সফার থিওরেম অনুযায়ী লোডে সর্বোচ্চ পাওয়ার ট্রান্সফার হবে তখনই যখন লোড রেজিস্ট্যান্স সোর্সের সাথে সংযুক্ত সিরিজ রেজিস্ট্যান্স বা সোর্সের অভ্যন্তরীণ রোধের সমান হবে।
১১। সুপারপজিশন থিওরেমে প্রতিটি রোধের কারেন্ট কয় বার নির্ণয় করতে হয় ?
উত্তর :- সুপারপজিশন থিওরেমে প্রতিটি রোধের কারেন্ট সর্বনিম্ন দুই (২) বার নির্ণয় করতে হয়।
১২। নর্টন তত্ত্বের সমতুল্য সার্কিটে কী সোর্স ব্যবহৃত হয় ?
উত্তর :- নটন থিওরেমের সমতুল্য সার্কিটে কারেন্ট সোর্স এবং থেভেনিন থিওরেমের সমতুল্য সার্কিটে ভোল্টেজ সোর্স ব্যবহৃত হয়।
১৩। ম্যাক্সিমাম পাওয়ার ট্রান্সফার থিওরেমটি লেখ।
উত্তর :- কোনো সোর্স হতে কোনো লোডে সর্বোচ্চ পাওয়ার ট্রান্সফার হবে তখনই যখন লোড রেজিস্ট্যান্স (এসি এর
ক্ষেত্রে ইম্পিড্যান্স) সোর্সের সাথে সংযুক্ত সিরিজ রেজিস্ট্যান্স (এসি এর ক্ষেত্রে ইম্পিড্যান্স)-এর সমান হবে।
১৪। সার্কিটের কোন্ অবস্থার প্রেক্ষিতে ‘সুপারপজিশন থিওরেম’ প্রয়োগ সুবিধাজনক ?
উত্তর :- যে-সকল সার্কিটে ই.এম.এফ-এর একাধিক উৎস থাকে, সে সকল সার্কিটের সমাধান ‘সুপারপজিশন সূত্র’ দ্বারাই সম্ভব।
১৫। নর্টন’স থিওরেমটি লেখ।
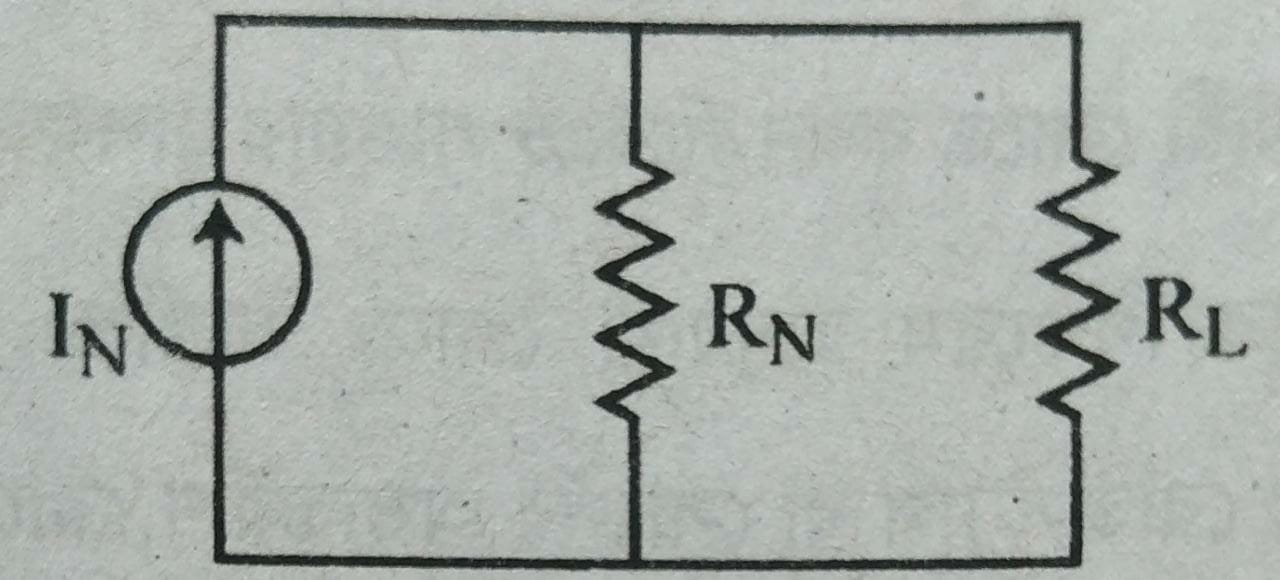
উত্তর :- “স্বতন্ত্র ভোল্টেজ এবং কারেন্ট উৎস (Source) বিশিষ্ট লিনিয়ার নেটওয়ার্কের দু’প্রান্ত (Terminals), একটি RN রেজিস্ট্যান্সের সাথে প্যারালালে একটি IN সমতুল্য কারেন্ট দ্বারা প্রতিস্থাপন (Replace) করা যেতে পারে;
যেখানে IN [নর্টন কারেন্ট] হলো প্রান্তদ্বয়ের শর্টসার্কিট কারেন্ট এবং RN (নর্টন রেজিস্ট্যান্স) হলো প্রান্তদ্বয় হতে পিছন দিকে নেটওয়ার্কের সমতুল্য রেজিস্ট্যান্স; কিন্তু শর্ত হলো ভোল্টেজ উৎসগুলো ‘শর্ট-সার্কিট’ এবং কারেন্ট উৎসগুলো ‘ওপেন- সার্কিট’ থাকতে হবে।”
১৬। নর্টন’স থিওরেম-এ শর্টসার্কিট কারেন্ট বলতে কী বুঝায় ?
উত্তর :- যে রেজিস্টরের মধ্যইদিয়ে প্রবাহিত কারেন্ট পরিমাপ করতে হবে, সে রেজিস্টরের দুই প্রান্তকে শর্ট করলে, শর্ট পথের মধ্য দিয়ে যে কারেন্ট প্রবাহিত হয়, তাকে শর্টসার্কিট কারেন্ট বলে।
১৭। থেভেনিন সমতুল্য বর্তনীতে কী সোর্স ব্যবহার করা হয় ?
উত্তর :- থেভেনিন সমতুল্য বর্তনীতে ভোল্টেজ সোর্স ব্যবহার করা হয়।
১৮। নর্টন’স থিওরেমে প্যারালাল সমতুল্য রেজিস্ট্যান্স বলতে কী বুঝায় ?
উত্তর :- অভ্যন্তরীণ রেজিস্ট্যান্স রেখে সকল ভোল্টেজ উৎস সরিয়ে ফেলতে হবে। অতঃপর যে শাখার কারেন্ট নির্ণয় করতে হবে তাকে খুলে ফেলতে হবে এবং খোলা প্রান্তদ্বয় হতে পশ্চাৎ দিকে নেটওয়ার্কের রেজিস্ট্যান্স নির্ণয় করতে হবে। একে নর্টন’স থিওরেমে প্যারালাল সমতুল্য রেজিস্ট্যান্স বলে।
১৯। নর্টন’স থিওরেম-এর সমতুল্য সার্কিট অঙ্কন কর।
উত্তর :- নিয়ে নর্টন’স থিওরেম-এর সমতুল্য সার্কিট অঙ্কন করা হলো :
২০। প্যারালালে সংযুক্ত ৪টি রোধ-এর সাথে আরো একটি রোধ প্যারালালে সংযোগ করলে সমতুল্য রোধ বৃদ্ধি পাবে, না কমে যাবে ?
উত্তর :- সমতুল্য রোধ কমে যাবে।
সংক্ষিপ্ত প্রশ্নোত্তর :
১। কারশফের কারেন্টের সূত্র ব্যাখ্যা কর।
উত্তর :- কোনো বৈদ্যুতিক নেটওয়ার্কে এক বিন্দুতে মিলিত কারেন্টসমূহের বীজগাণিতিক যোগফল শূন্য হয়।” অথবা, “কোনো বৈদ্যুতিক নেটওয়ার্কের একটি সংযোগস্থলে আগত কারেন্টসমূহের বীজগাণিতিক যোগফল, ঐ সংযোগস্থল হতে নির্গত কারেন্টসমূহের বীজগাণিতিক যোগফলের সমান।” চিত্রে পাঁচটি পরিবাহী তারকে একটি বিন্দুতে [O] সংযোগ করা হয়েছে। ধরা যাক, I1, I2, I3, I ও I, কারেন্ট উক্ত তার দিয়ে প্রবাহিত হচ্ছে। I ও I3
কারেন্টসমূহ O সংযোগস্থল হতে নির্গত হচ্ছে এবং I2, I ও I, কারেন্টসমূহ O সংযোগস্থলে আগমন করছে।
সংযোগস্থলে আগত কারেন্টসমূহকে পজিটিভ এবং নির্গত কারেন্টসমূহকে নেগেটিভ চিহ্ন দ্বারা সূচিত করলে, সূত্রানুযায়ী—
( – I) + I2 + (- I3) + L + I5 = 0
বা, – I1 + I2 – I3 + I4 + I5 = 0
I2 +I4 + I5 = I1 + I3
অর্থাৎ, আগত কারেন্ট = নির্গত কারেন্ট

২। কারশফের ভোল্টেজের সূত্রটি ব্যাখ্যা কর।
উত্তর :- “কোনো ঘেরা বা বদ্ধ (Closed) বৈদ্যুতিক সার্কিটে সকল ই.এম.এফ. (E.M.F) এবং সকল ভোল্টেজ-ড্রপের বীজগাণিতিক যোগফল শূন্য হয়। ”
উপরোক্ত বদ্ধ সার্কিটে (চিত্র : দ্রষ্টব্য) তিনটি লুপ আছে, যথা- ABCFA, EDCFE এবং ABCDEFA.
কারশফের দ্বিতীয় সূত্র বা ভোল্টেজ সূত্র প্রয়োগ করে, আমরা তিনটি বদ্ধ লুপে তিনটি সমীকরণ পেতে পারি-
১। ABCFA লুপ-এ
E-IR, IR, 0
২। EDCFE লুপ-এ
E2 – I2R2 – I3 R3 = 0
৩। ABCDEFA লুপ-এ
E – I R + I2 R 2 – E2 = 0
৩। কারশফের সূত্র এবং ম্যাক্সওয়েলের সূত্রের পার্থক্য লেখ।
উত্তর :- কারশফের সূত্রে প্রত্যেকটি ব্রাঞ্চ বা শাখায় পৃথক পৃথক কারেন্ট ধরে প্রতিটি জাংশন বা নোডে কারেন্ট সূত্রের সাহায্যে শাখা কারেন্টের সমীকরণ লিখতে হয়। পরে প্রতিটি লুপ বা অংশে ভোল্টেজ সূত্রের সাহায্যে ভোল্টেজ সমীকরণ লিখতে হয়। ম্যাক্সওয়েলের সূত্রের লুপ বা অংশে কারশফের ভোল্টেজ সূত্র অনুযায়ী সমীকরণ লিখতে হয়,
আর ম্যাক্সওয়েলের সূত্রে আলাদা আলাদা লুপ বা অংশে আলাদাভাবে কারেন্ট নির্ণয় করতে হয়। আসল কথা, দুটি সূত্রেই পার্থক্য হলো কারশফের বেলায় প্রতিটি শাখায় আলাদাভাবে কারেন্ট ধরতে হয়, আর ম্যাক্সওয়েলের বেলায় প্রতিটি লুপে বা অংশে আলাদাভাবে কারেন্ট বিবেচনা করতে হয়।
৪। থেভেনিন’স থিওরেম বর্ণনা কর।
উত্তর :- “ই.এম.এফ-এর একাধিক উৎস এবং রেজিস্ট্যান্স সমন্বয়ে গঠিত একটি জটিল নেটওয়ার্কের দু’টি বিন্দুতে সংযুক্ত একটি লোড রেজিস্টরে কারেন্ট একই হবে, যেন লোডটি ই.এম.এফ-এর একটিমাত্র স্থির উৎসের সাথে সংযুক্ত যার ই.এম.এফ. লোডের আড়াআড়িতে
‘ওপেন সার্কিট ভোল্টেজ’-এর সমান এবং যার অভ্যন্তরীণ রেজিস্ট্যান্স দু’টি প্রান্ত হতে পশ্চাৎ দিকের নেটওয়ার্কের রেজিস্ট্যান্সের সমান। ই.এম.এফ-এর উৎসগুলো তাদের সমতুল্য অভ্যন্তরীণ রেজিস্ট্যান্স দ্বারা স্থলাভিষিক্ত হয়।”
৫ । সুপারপজিশন থিওরেম বর্ণনা কর।
উত্তর :- কোনো লিনিয়ার বাইল্যাটারাল নেটওয়ার্কে একটি বিন্দুতে প্রবাহিত কারেন্ট অথবা দুটি বিন্দুতে পটেনশিয়ালের পার্থক্য ই.এম.এফ-এর একাধিক উৎসের কারণে ঐ বিন্দু অথবা বিন্দুগুলোতে প্রবাহিত পৃথক পৃথক কারেন্টসমূহের অথবা পটেনশিয়ালের পার্থক্যসমূহের বীজগাণিতিক যোগফলের সমান হবে,
যদি প্রতিটি উৎসকে পৃথকভাবে বিবেচনা করা এবং অন্য উৎসগুলোর প্রত্যেকটি সমমানের অভ্যন্তরীণ রেজিস্ট্যান্সে রূপান্তরিত করা হয়।
৬। নর্টন’স থিওরেম বর্ণনা কর।
উত্তর :- স্বতন্ত্র ভোল্টেজ ও কারেন্ট উৎসবিশিষ্ট লিনিয়ার নেটওয়ার্কের দু’প্রান্ত, একটি RN [নর্টন রেজিস্ট্যান্স] রেজিস্ট্যান্সের সাথে প্যারালালে একটি IN (নর্টন কারেন্ট] সমতুল্য কারেন্ট দ্বারা প্রতিস্থাপন করা যেতে পারে;
যেখানে In হলো প্রান্তদ্বয়ের শর্টসার্কিট কারেন্ট এবং RN হলো প্রান্তদ্বয় হতে পিছন দিকে নেটওয়ার্কের সমতুল্য রেজিস্ট্যান্স; কিন্তু শর্ত হলো ভোল্টেজ উৎসগুলো ‘শর্টসার্কিট’ এবং কারেন্ট উৎসগুলো ‘ওপেন সার্কিট’ থাকতে হবে।
৭। থেভেনিন থিওরেম-এর মাধ্যমে কোনো জটিল নেটওয়ার্কের সমস্যা সমাধানে যে-সকল ধাপ অতিক্রম করতে হয়, তা ধারাবাহিকভাবে লেখ ।
উত্তর :-
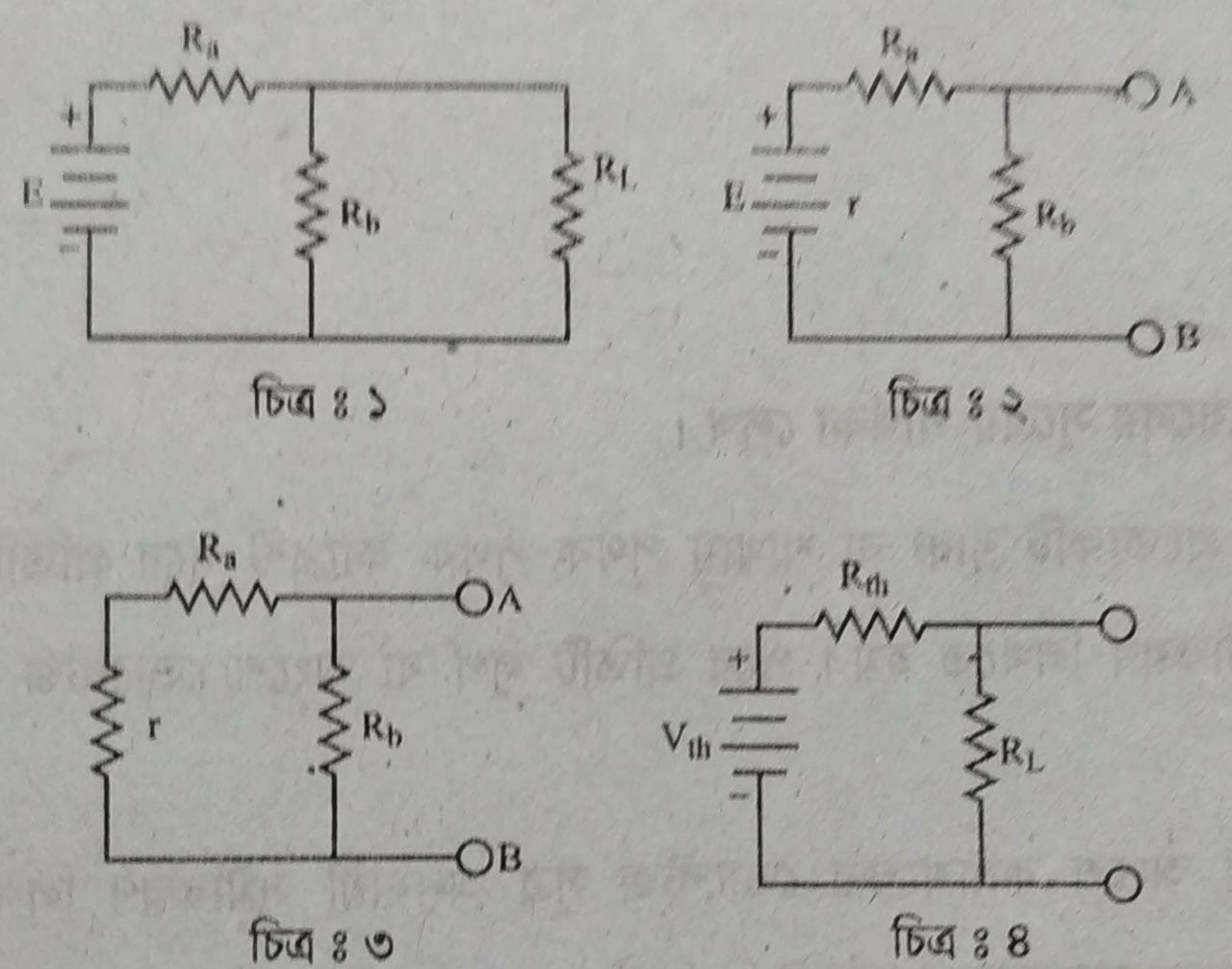
থেভেনিন’স থিওরেম ব্যবহার করে সার্কিট সমাধানের কৌশল :
১। প্রথমেই সার্কিট (চিত্র-১) থেকে RL কে বিচ্ছিন্ন করতে হবে এবং সেই স্থান open রাখতে হবে (চিত্র-২)।
২। এবার সোর্সকে শর্ট করতে হবে। যদি Internal Resistance থাকে তাহলে সোর্সের স্থানে সেই রেজিস্ট্যান্স দ্বারা সংযুক্ত করতে হবে (চিত্র-৩) ।
৩। এবার RAB নির্ণয় করতে হবে। : RAB = Ro
৪। এবার I নির্ণয় করতে হবে এবং পরে Vab নির্ণয় করতে হবে। Vab = IbxRy, Vab = Vh
৫। এখন একটি নতুন সার্কিট তৈরি করতে হবে, যেখানে সোর্স হিসাবে Via থাকবে এবং ঐ সার্কিটে Run সিরিজে থাকবে।
৬। এবার Ra ও RL সিরিজ হয়ে Vin এর সাথে প্যারালালে থাকবে (চিত্র-৪)।
৮। নর্টন থিওরেমের সাহায্যে একটি নেটওয়ার্কের সমাধান কীভাবে করা হয়, লেখ।
উত্তর :-

১। প্রথমেই প্রদত্ত দু’টি প্রান্তের আড়াআড়ি হতে রেজিস্ট্যান্স সরিয়ে ফেলতে হবে এবং তদস্থলে একটি শর্টসার্কিট বসাতে হবে।
২। এরপর শর্টসার্কিট কারেন্ট IN নির্ণয় করতে হবে।
৩। অভ্যন্তরীণ রেজিস্ট্যান্স রেখে সকল ভোল্টেজ উৎস সরিয়ে ফেলতে হবে। তদ্রূপ সকল কারেন্ট উৎস সরিয়ে তদস্থলে ওপেন সার্কিট অর্থাৎ অসীম রেজিস্ট্যান্স রাখতে হবে।
৪। এরপর প্রদত্ত প্রান্তদ্বয় হতে পশ্চাৎ দিকে নেটওয়ার্কের রেজিস্ট্যান্স Rs নির্ণয় করতে হবে। ৫। এখন প্রদত্ত প্রান্তদ্বয়ের মধ্যবর্তী RN-এর আড়াআড়ি প্যারালালে সংযুক্ত কারেন্ট উৎস (Is) হবে নর্টনের সমতুল্য সার্কিট।
৯। কারশফের সূত্র কীভাবে সমাধান করতে হয়, তা ধারাবাহিকভাবে লেখ।
উত্তর :-
১। সার্কিটের একটি পরিচ্ছন্ন চিত্র আঁকতে হবে।
২। সকল সংযোগস্থল (Junction-point) অক্ষর দ্বারা চিহ্নিত করতে হবে, যাতে কারেন্ট পরিক্রমার বিভিন্ন পথ শনাক্ত করা যায়।
৩। ই.এম.এফ-এর উৎসগুলোর জাত ভোল্টেজ এবং মেরু (Polarity) যথাযথ চিহ্ন দ্বারা নির্দেশ করতে হবে।
8। সকল রেজিস্ট্যান্সের মান যথাস্থানে বসাতে হবে।
৫। কারেন্ট বিতরণের সবচেয়ে সম্ভাব্য দিক বা অভিমুখ, তীর-চিহ্ন দ্বারা নির্দেশ করতে হবে এবং সকল জ্ঞাত মান বসাতে হবে।
৬। উপযুক্ত অক্ষর দ্বারা সার্কিটের অজ্ঞাত ধ্রুবকগুলো শনাক্ত করতে হবে (E2. Rs, I, ইত্যাদি)। সংযোগস্থলে কারশফের কারেন্ট সূত্র প্রয়োগের বেলায় অজ্ঞাত ধ্রুবকের সংখ্যা যত কম রাখা যায়, ততই ভালো।
৭। কারশফের ভোল্টেজ সূত্র প্রয়োগকালে, কোনো একটি সম্পূর্ণ পথ অনুসরণ করে ভোল্টেজের সমীকরণ লিখতে হবে। এভাবে যতগুলো অজানা ধ্রুবক আছে, এদের পথ চিহ্নিত করে সমীকরণ লিখতে হবে।
৮। ধারাবাহিকভাবে সমীকরণগুলোর সমাধান করতে হবে।
